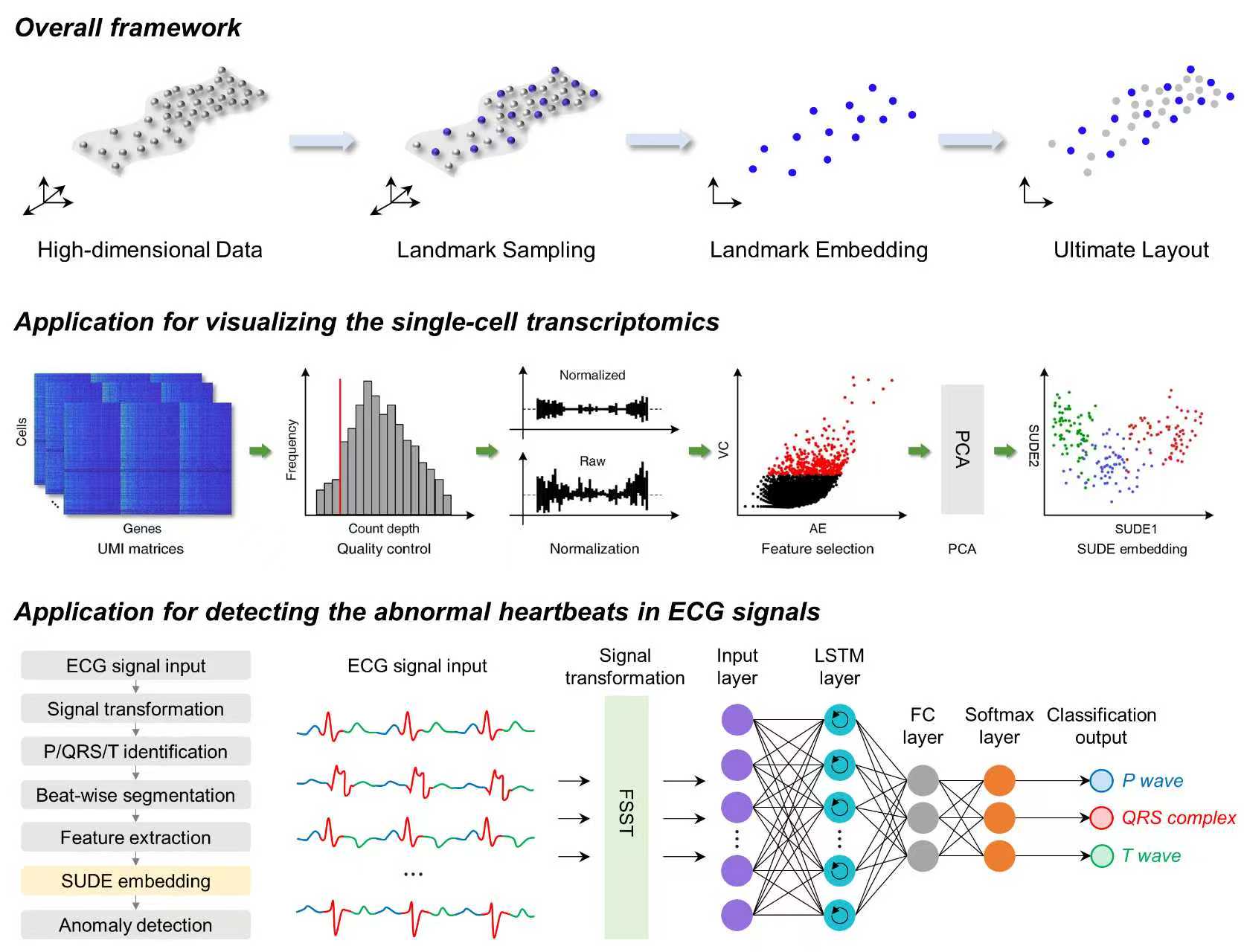
Sampling-enabled scalable manifold learning unveils the discriminative cluster structure of high-dimensional data (SUDE)

We propose a scalable manifold learning (SUDE) method that can cope with large-scale and high-dimensional data in an efficient manner. It starts by seeking a set of landmarks to construct the low-dimensional skeleton of the entire data, and then incorporates the non-landmarks into this skeleton based on the constrained locally linear embedding. This project provides the Python version of SUDE, and the MATLAB version can be found at https://github.com/ZPGuiGroupWhu/sude. This paper has been published in Nature Machine Intelligence, and more details can be seen https://www.nature.com/articles/s42256-025-01112-9.

Installation

Supported python versions are 3.8 and above.

This project has been uploaded to PyPI, supporting direct download and installation from pypi

pip install sude

Manual Installation

git clone https://github.com/ZPGuiGroupWhu/SUDE-pkg.git
cd SUDE-pkg
pip install -e .

How To Run

The SUDE algorithm package provides the sude function for clustering.

The description of the hyperparameters for user configuration are presented as follows

def sude(
    X,
    no_dims = 2,
    k1 = 20,
    normalize = True,
    large = False,
    initialize = 'le',
    agg_coef = 1.2,
    T_epoch = 50,
):
"""
    This function returns representation of the N by D matrix X in the lower-dimensional space. Each row in X
    represents an observation.

    Parameters are:

    'no_dims'      - A positive integer specifying the number of dimension of the representation Y.
                   Default: 2
    'k1'           - A non-negative integer specifying the number of nearest neighbors for PPS to
                   sample landmarks. It must be smaller than N.
                   Default: adaptive
    'normalize'    - Logical scalar. If true, normalize X using min-max normalization. If features in
                   X are on different scales, 'Normalize' should be set to true because the learning
                   process is based on nearest neighbors and features with large scales can override
                   the contribution of features with small scales.
                   Default: True
    'large'        - Logical scalar. If true, the data can be split into multiple blocks to avoid the problem
                   of memory overflow, and the gradient can be computed block by block using 'learning_l' function.
                   Default: False
    'initialize'   - A string specifying the method for initializing Y before manifold learning.
        'le'       - Laplacian eigenmaps.
        'pca'      - Principal component analysis.
        'mds'      - Multidimensional scaling.
                   Default: 'le'
    'agg_coef'     - A positive scalar specifying the aggregation coefficient.
                   Default: 1.2
    'T_epoch'      - Maximum number of epochs to take.
                   Default: 50
"""

After installing the SUDE library, you can use this function as follows:

import pandas as pd
import numpy as np
from sude import sude
import time
import matplotlib.pyplot as plt

# Input data
data = np.array(pd.read_csv('benchmarks/rice.csv', header=None))

# Obtain data size and true annotations
m = data.shape[1]
X = data[:, :m - 1]
ref = data[:, m - 1]

# Perform SUDE embedding
start_time = time.time()
Y = sude(X, k1=10)
end_time = time.time()
print("Elapsed time:", end_time - start_time, 's')

plt.scatter(Y[:, 0], Y[:, 1], c=ref, cmap='tab10', s=4)
plt.show()

Citation Request

Peng, D., Gui, Z., Wei, W. et al. Sampling-enabled scalable manifold learning unveils the discriminative cluster structure of high-dimensional data. Nat. Mach. Intell. (2025). https://doi.org/10.1038/s42256-025-01112-9

License

SUDE is released under the MIT License.